Monte Carlo Mathematica Code

A sequence of random numbers can be a very simple monte carlo simulation.

Monte carlo mathematica code. He said that a mathematica program could be created that would perform the operations. Mathematica package containing a general purpose markov chain monte carlo routine i wrote. This method is particularly useful for higher dimensional integrals. We were very interested in exploring the idea of using a monte carlo method to evaluate definite integrals.

Monte carlo simulations can be constructed directly by using the wolfram language s built in random number generation functions. This is the heart of the monte carlo technique. Here is a fragment of mathematica code implementing the above. Generate a random number between zero and one.

The reason the code is so slow is that it s very expensive to calculate scatter angles like this 38 ms per call on my computer. Includes various examples and documentation. Since we wanted to test the accuracy and precision of the method it was necessary to design a program that would perform the procedure several times. If the value of the gaussian is greater than the random number keep the value of x.

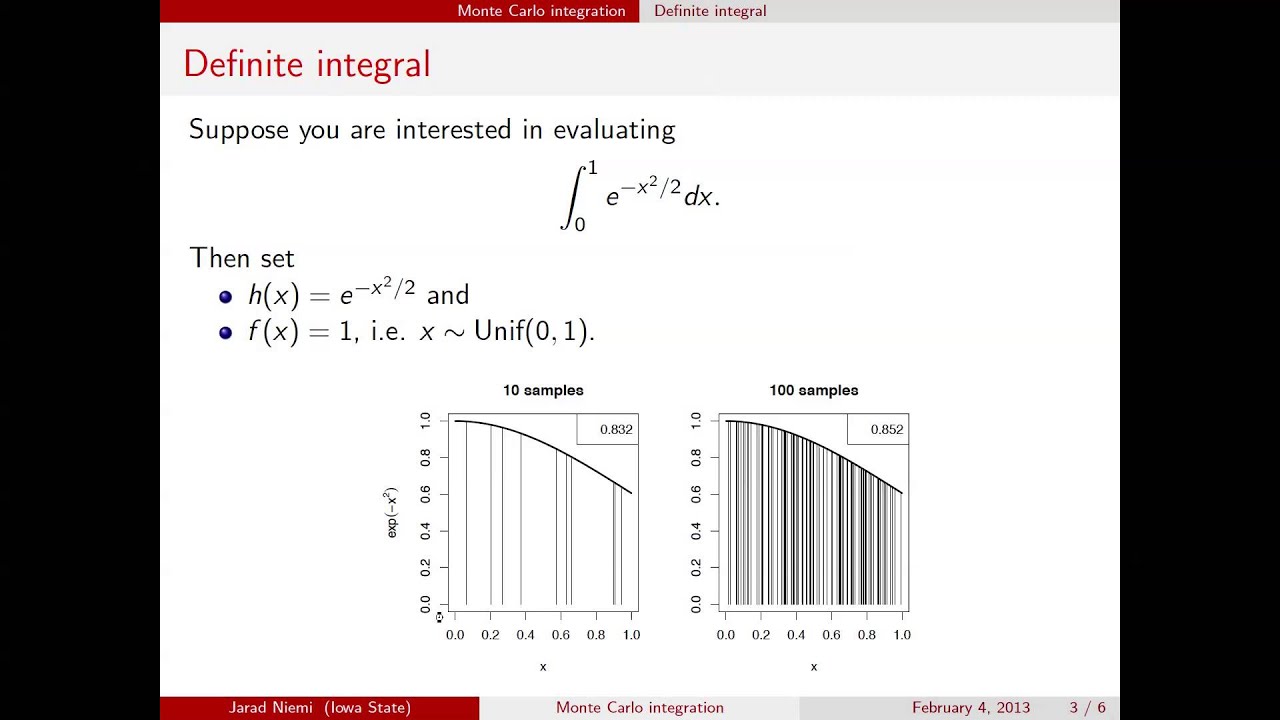
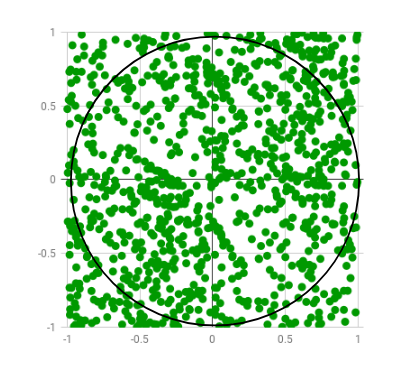
In mathematics monte carlo integration is a technique for numerical integration using random numbers it is a particular monte carlo method that numerically computes a definite integral while other algorithms usually evaluate the integrand at a regular grid monte carlo randomly chooses points at which the integrand is evaluated. Mathematica markov chain monte carlo. We assume here that eda is loaded so we can use the gaussian. Current monte carlo walk simulation without if statement randomwalk n accumulate prepend randomvariate custom a n 0 listlineplot table randomwalk 10 5.